7 אלגוריתמים שכל מתכנת צריך לדעת

כתלמיד לתכנות, סביר להניח שלמדת המון אלגוריתמים שונים במהלך הקריירה שלך. התמחות באלגוריתמים שונים היא חיונית בהחלט עבור כל מתכנת.

עם כל כך הרבה אלגוריתמים, זה יכול להיות מאתגר לעקוב אחר מה חיוני. אם אתם מתכוננים לראיון או פשוט מברקים את הכישורים שלכם, הרשימה הזו תקל על זה יחסית. המשך לקרוא בעודנו מפרטים את האלגוריתמים החיוניים ביותר למתכנתים.

1. האלגוריתם של דיקסטרה

אדסגר דייקסטרה היה אחד ממדעני המחשב המשפיעים ביותר בתקופתו, והוא תרם לכך תחומים רבים ושונים של מדעי המחשוב, כולל מערכות הפעלה, בניית מהדרים, והרבה יותר. אחת התרומות הבולטות של דיקסטרה היא כושר ההמצאה של אלגוריתם הנתיב הקצר ביותר שלו לגרפים, המכונה גם אלגוריתם הנתיב הקצר ביותר של דיקסטרה.

האלגוריתם של דיקסטרה מוצא את הנתיב הקצר ביותר בגרף ממקור לכל קודקודי הגרף. על כל איטרציה של האלגוריתם, מתווסף קודקוד עם המרחק המינימלי מהמקור וכזה שאינו קיים בנתיב הקצר ביותר הנוכחי. זהו הנכס החמדני המשמש את האלגוריתם של Djikstra.

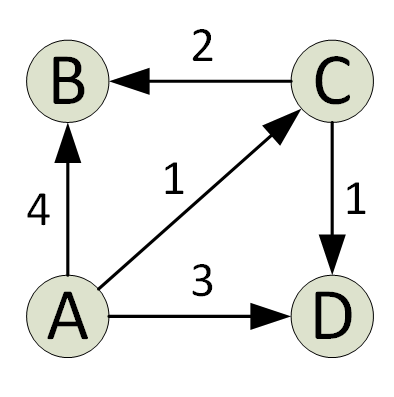
האלגוריתם מיושם בדרך כלל באמצעות קבוצה. האלגוריתם של דיקסטרה יעיל מאוד כאשר הוא מיושם עם ערימת דקות; אתה יכול למצוא את הנתיב הקצר ביותר בזמן O (V+ElogV) בלבד (V הוא מספר הקודקודים ו- E הוא מספר הקצוות בגרף נתון).

לאלגוריתם של דיקסטרה יש מגבלות; הוא פועל רק על גרפים מכוונים ובלתי מכוונים עם קצוות בעלי משקל חיובי. עבור משקולות שליליות, אלגוריתם בלמן-פורד עדיף בדרך כלל.

שאלות הראיון כוללות בדרך כלל את האלגוריתם של Djikstra, לכן אנו ממליצים בחום להבין את הפרטים והיישומים המורכבים שלו.

2. מיזוג מיון

יש לנו כמה אלגוריתמי מיון ברשימה זו, ומיון מיזוג הוא אחד האלגוריתמים החשובים ביותר. זהו אלגוריתם מיון יעיל המבוסס על טכניקת התכנות Divide and Conquer. בתרחיש הגרוע ביותר, מיון מיזוג יכול למיין מספרים "n" בזמן O (nlogn) בלבד. לעומת טכניקות מיון פרימיטיביות כגון מיון בועות (זה לוקח זמן O (n^2)), מיון המיזוג יעיל מצוין.

קָשׁוּר: מבוא לאלגוריתם מיון המיזוג

במיון מיזוג, המערך למיון מתפרק שוב ושוב למערכי משנה עד שכל מערך משנה מורכב ממספר בודד. האלגוריתם רקורסיבי לאחר מכן ממזג שוב ושוב את מערכי המשנה וממיין את המערך.

3. Quicksort

Quicksort הוא אלגוריתם מיון נוסף המבוסס על טכניקת התכנות Divide and Conquer. באלגוריתם זה, אלמנט נבחר תחילה כציר, ואז המערך כולו מחולק סביב ציר זה.

כפי שבטח ניחשתם, ציר טוב הוא חיוני למיון יעיל. הציר יכול להיות אלמנט אקראי, אלמנט המדיה, האלמנט הראשון או אפילו האלמנט האחרון.

יישומים של מבחר קוויקס שונים לעתים קרובות באופן בו הם בוחרים ציר. במקרה הממוצע, quicksort ימיין מערך גדול עם ציר טוב בזמן O (nlogn) בלבד.

הפסאודוקוד הכללי של quicksort מחלק שוב ושוב את המערך על הציר וממקם אותו במיקום הנכון של מערך המשנה. הוא גם ממקם את האלמנטים הקטנים מהציר משמאלו ואת האלמנטים הגדולים יותר מהציר מימין.

4. עומק חיפוש ראשון

עומק חיפוש ראשון (DFS) הוא אחד מאלגוריתמי הגרף הראשונים הנלמדים לתלמידים. DFS הוא אלגוריתם יעיל המשמש לחצות או לחפש גרף. ניתן גם לשנות אותו לשימוש בחציית עצים.

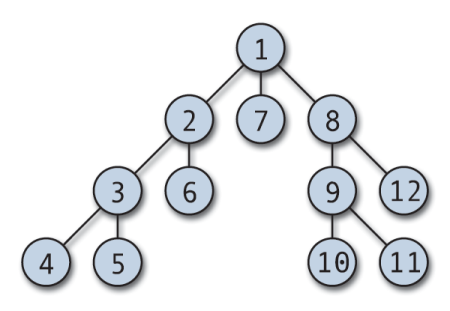
מעבר DFS יכול להתחיל מכל צומת שרירותי, והוא צולל לכל קודקוד סמוך. האלגוריתם חוזר אחורה כשאין קודקוד בלתי מבוקר, או שיש מבוי סתום. DFS מיושם בדרך כלל עם מחסנית ומערך בוליאני כדי לעקוב אחר הצמתים שביקרו בהם. DFS פשוט ליישום ויעיל במיוחד; זה עובד (V+E), כאשר V הוא מספר הקודקודים ו- E הוא מספר הקצוות.

יישומים אופייניים לחציית DFS כוללים מיון טופולוגי, איתור מחזורים בגרף, איתור נתיבים ומציאת רכיבים המחוברים חזק.

5. רוחב-חיפוש ראשון

Breadth-First Search (BFS) ידועה גם בתור מעבר סדר ברמה לעצים. BFS פועל ב- O (V+E) בדומה לאלגוריתם DFS. עם זאת, BFS משתמש בתור במקום הערימה. DFS צולל לתוך הגרף, בעוד BFS חוצה את הגרף לרוחב.

אלגוריתם BFS משתמש בתור כדי לעקוב אחר הקודקודים. קודקודים סמוכים לא מבוקרים מבקרים, מסומנים ובתור. אם לקודקוד אין קודקוד סמוך, אז קודקוד מוסר מהתור ונחקר.

BFS נפוץ ברשתות peer-to-peer, הנתיב הקצר ביותר של גרף לא משוקלל, וכדי למצוא את העץ המינימלי המשתרע.

6. חיפוש בינארי

חיפוש בינארי הוא אלגוריתם פשוט למציאת האלמנט הנדרש במערך ממוין. הוא פועל על ידי חלוקת המערך שוב ושוב לשניים. אם האלמנט הנדרש קטן מהאלמנט הבינוני ביותר, אז הצד השמאלי של האלמנט האמצעי מעובד הלאה; אחרת הצד הימני חצוי וחוזר שוב. התהליך חוזר על עצמו עד שנמצא האלמנט הנדרש.

מורכבות הזמן הגרוע ביותר של חיפוש בינארי היא O (logg) מה שהופך אותו ליעיל מאוד בחיפוש מערכים לינארים.

7. אלגוריתמים מינימליים של עץ משתרע

לעץ משתרע מינימלי (MST) של גרף יש את העלות המינימלית בין כל העצים המתפרשים האפשריים. עלותו של עץ משתרע תלויה במשקל הקצוות שלו. חשוב לציין שיכול להיות יותר מעץ מינימלי אחד המשתרע. ישנם שני אלגוריתמים עיקריים של MST, כלומר של Kruskal ו- Prim.

האלגוריתם של Kruskal יוצר את ה- MST על ידי הוספת הקצה בעלות מינימלית לסט הולך וגדל. האלגוריתם ממיין תחילה קצוות לפי משקלן ולאחר מכן מוסיף קצוות ל- MST החל מהמינימום.

חשוב לציין כי האלגוריתם אינו מוסיף קצוות היוצרים מחזור. האלגוריתם של קרוסקל מועדף לגרפים דלילים.

האלגוריתם של Prim משתמש גם במאפיין חמדני והוא אידיאלי עבור גרפים צפופים. הרעיון המרכזי ב- MST של Prim הוא שיהיו שתי קבוצות קודקודים מובחנות; קבוצה אחת מכילה את ה- MST הגדל, ואילו השנייה מכילה קודקודים שאינם בשימוש. בכל איטרציה נבחר קצה המשקל המינימלי שיחבר בין שתי הסטים.

אלגוריתמים מינימליים של עץ הם חיוניים לניתוח אשכולות, טקסונומיה ורשתות שידור.

מתכנת יעיל בקיא באלגוריתמים

מתכנתים כל הזמן לומדים ומפתחים את כישוריהם, ויש כמה יסודות בסיסיים שכולם צריכים להיות בקיאים בהם. מתכנת מיומן מכיר את האלגוריתמים השונים, את היתרונות והחסרונות של כל אחד ואילו אלגוריתם יתאים ביותר לתרחיש נתון.

מבוא לאלגוריתם מיון המעטפת

אמנם מיון קליפות אינו השיטה היעילה ביותר, אך למתחילים יש הרבה מה להרוויח מתרגול זה.

קרא הבא

על הסופר